1 ディープラーニング
1.1 環境の準備
ディープラーニングにも対応した機械学習ライブラリである「Tensorflow」の環境を構築します。
pip install tensorflow
1.2 ニューラルネットワークとは？
ニューラルネットワークとは、人間の脳の神経細胞（ニューロン）の動作を参考に作られた計算モデルです。
ニューロンは複数の入力信号を受け取り、それらの総和が閾値を超えると出力信号を発火します。
パーセプトロンはこれを模した簡単なモデルで、入力データにある数を掛けます。これを重み付けといいます。それらを合計し、バイアス以上であれば 1 を、そうでなければ 0 を出力します。
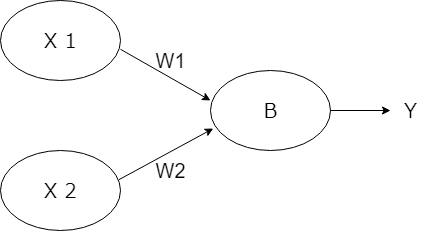
例えば、and出力をパーセプトロンで表してみます。 引数 x1とx2には1または0が入ってくるものとします。これに重み付け係数（w1とw2）を掛けて、バイアス（0.5）以上なら1、そうじゃないなら0を返します。
deep_per.ipynb に以下を記述してみましょう。
# ANDの例
def percep(x1, x2):
w1 = 0.3 # 重み１
w2 = 0.3 # 重み２
b = 0.5 # バイアス
a = x1 * w1 + x2 * w2
if a >= b:
y = 1
else:
y = 0
return y # 出力
print(percep(0, 0))
print(percep(0, 1))
print(percep(1, 0))
print(percep(1, 1))
この関数は重み付け係数とバイアスを変えるだけでORにすることもできます。重み付け係数を0.5、バイアスを0.3にするだけです。NANDにするには、重み付け係数を-0.5、バイアスを-0.7にします。
このように、重み付け係数とバイアスを変更することで、さまざまな処理を行えるようにします。
1.3 多層ニューラルネットワーク
ニューラルネットワークはこのパーセプトロンをいくつもつなげます。そして最終的に０か１かの数値にします。
例えば、XORは一つのパーセプトロンでは実現できません。ANDとNANDの結果をORすることでXORを実現します。
def and_gate(x1, x2):
w1 = 0.3
w2 = 0.3
b = 0.5
a = x1 * w1 + x2 * w2
return 1 if a >= b else 0
def or_gate(x1, x2):
w1 = 0.5
w2 = 0.5
b = 0.3
a = x1 * w1 + x2 * w2
return 1 if a >= b else 0
def nand_gate(x1, x2):
w1 = -0.5
w2 = -0.5
b = -0.7
a = x1 * w1 + x2 * w2
return 1 if a >= b else 0
def xor_gate(x1, x2):
# 1層目: NANDゲートとORゲートで出力を計算
nand_output = nand_gate(x1, x2)
or_output = or_gate(x1, x2)
# 2層目: NANDゲートとORゲートの出力をANDゲートに統合
xor_output = and_gate(nand_output, or_output)
return xor_output
# テスト
print(xor_gate(0, 0)) # 出力: 0
print(xor_gate(0, 1)) # 出力: 1
print(xor_gate(1, 0)) # 出力: 1
print(xor_gate(1, 1)) # 出力: 0
このように複数のパーセプトロンを組み合わせ、複雑なことが可能になります。
1.4 ディープラーニング
例えば、あやめの分類を行うとします。
４つの数値が入力です（SepalLength、SepalWidth、PetalLength、PetalWidth）。これを入力として最終的に３つの出力（３種類のどれか）を得ます。この３つの出力がそれぞれその答えになる確率が入ります。
ニューラルネットワークでは、学習データを使い、正解との誤差を最小化するように重みとバイアスを調整します。この作業が「学習」です。
ニューラルネットワークは画像認識にも適用できます。
画像はピクセル値の行列（数値配列）として表現でき、例えば 8×8 のグレースケール画像なら64個の数値で表されます。これを入力として、最終的に 10 個の要素を持つ出力（数字0～9の確率）を得ることができます。
これを多重に行っていきます。一番最初が入力層、最後が出力層と呼ばれます。中間は中間層（隠れ層）と呼ばれます。この中間層を大量に設けて処理するのがディープニューラルネットワーク、つまりディープラーニングです。