Python 機械学習主成分分析

データの傾向

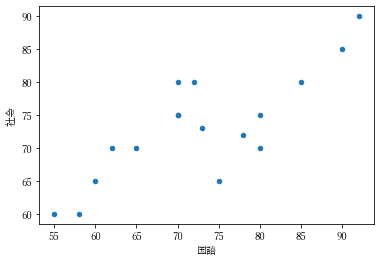
列がいくつもある場合、散布図を書くためには多数の組み合わせが生じ、全体的にどのようなデータが多いのか、傾向がわかりにくくなります。

import pandas as pd
import matplotlib.pyplot as plt

df = pd.read_csv("seiseki.csv")
# 国語、算数、社会、理科があるが、とりあえず国語と社会のみ
df.plot.scatter(x='国語', y='社会')

そこでいくつかの列をまとめて１つの軸にすることで、列を削減することができます。これを次元削減といい、その方法が主成分分析です。

PCAというアルゴリズムを使い、次元を２つにまで削減します。

df = df.drop(columns=['名前','クラス','性別'])

from sklearn.decomposition import PCA
model = PCA(n_components=2, whiten=True)
model.fit(df)

n_components=2を指定することで列が２つになりました。
それをDataFrameで表示してみます。

new_data = model.transform(df) # numpyで取得
new_df = pd.DataFrame(new_data) # numpyをDataFrameに
new_df # 新たな2軸のDataFrame

新たな軸の傾向を見て名前を付けます。

仮にPC1、PC2と付けて元のDataFrameと結合してみます。

new_df.columns = ['PC1','PC2']
df2 = pd.concat([df, new_df], axis=1)
df2

相関を得ます。

df_corr = df2.corr()
pc_corr = df_corr.loc[:'理科', 'PC1':] # 理科より上の行、PC1より右の列
pc_corr

PC1の列を降順に並べ替えて表示します。

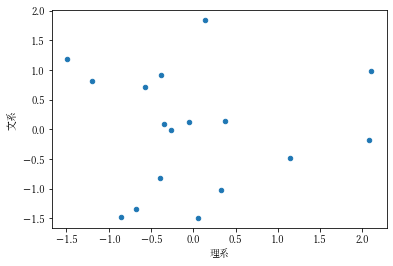
pc_corr['PC1'].sort_values(ascending=False)

# 結果
理科    0.878230
算数    0.790551
国語    0.629135
社会    0.409901

理科と算数が強い相関がありますので「理系」と名付けます。

次のPC2の列を降順に並べ替えて表示します。

pc_corr['PC2'].sort_values(ascending=False)

# 結果
社会    0.817763
国語    0.753478
理科   -0.283917
算数   -0.574894

社会と国語と強い正の相関、算数が負の相関がありますので「文系」と名付けます。

これを散布図で示してみます。

new_df.columns = ['理系', '文系']
new_df.plot.scatter(x='理系', y='文系')